Hmm, you sure we aren't saying the same thing? To use the terms as I understand them, A Mobius Loop is a non-orientable manifold of 1 dimension fewer than a Klein Bottle, yeah? Just as there's no distinction between the top and bottom of a 3D Mobius Loop, there's no distinction between the inside and outside of a true 4D Klein Bottle. In 3D, it's just warped a bit funny, due to not being able to extend the surface out/in in that direction.
It's just as possible that I don't get the distinction you're pointing out here, though. I'm in no way classically-trained, and my grasp of formal terminology is pretty sparse.
Naah, both the Möbius strip and the Klein bottle are two-dimensional manifolds - they locally look like the two-dimensional real plane, after all. What's important is that they are
abstract objects - they're separate from their
embedding into three- or four-dimensional space. What you're calling 'warped a bit funny' is the observation that the Klein bottle cannot be properly embedded into three-dimensional space; trying to do so comes at the price of self-intersection. It's very important that the self-intersecting object you get
no longer is a Klein bottle, or even just a manifold at all!
It's rather counterproductive to cling to this sort of visualization anyway. Here is a more elegant way to think about Klein bottles and Möbius strips, which makes several of the glueing statements in the thread fairly easy to see:
Möbius strip:

Klein bottle:
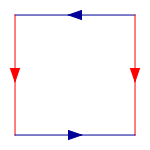
Torus:

You get the space in question by glueing together the same-colored arrows in the same direction. Try it out with the torus - it's rather odd at first, but you'll get used to it rather quickly. Then ask yourself: What object do I get if I cut out a horizontal band of height 1/2 out of the middle of the Klein bottle diagram?
'Morally', as my topology prof would say, the comparison between Möbius strip and Klein bottle that you make is correct. However it's hard to make it rigorous: You're looking at the boundary of the Möbius strip, but the Klein bottle does not have a boundary. The better comparison is: Just as you cannot distinguish front and back of a Möbius strip, you cannot distinguish between the inside and the outside of a Klein bottle - that's basically what non-orientability is. In fact that's precisely what you see if cut out a piece of a Klein bottle that looks like a Möbius strip, as in the spoiler above. Generalizing this, a surface is non-orientable iff you can embed a Möbius strip into it, and I think similar statements hold in higher dimensions.
The whole orientability thing gives rise to a lot of interesting topology - look into differential topology and the transversality theory in particular if you want more of this


 Author
Topic: SCIENCE, Gravitational waves, and the whole LIGO OST! (Read 482788 times)
Author
Topic: SCIENCE, Gravitational waves, and the whole LIGO OST! (Read 482788 times)
